Blog
Assignments are sometimes fun.
Not Every CNF is the Same
A boolean formula is a four-occurence CNF formula if it is in conjunctive normal form and every variable appears at most 4 times. Define
\[{\sf CNF_4} = \{\psi : \psi \text{ is a satisfiable, four-occurrence CNF formula}\}\]It is well known that \({\sf CNF_4}\) is \({\cal NP}\)-complete. But consider a four-occurence 4CNF formula, which is in conjunctive normal form, and every variable appears at most four times, and every clause contains exactly four literals. Define
\[{\sf 4CNF_4} = \{\phi : \phi \text{ is a satisfiable, four-occurrence 4CNF formula}\}\]It turns out that \({\sf 4CNF_4}\) is in \({\cal P}\)! It turns out that \({\sf 4CNF_4}\) can be formulated into a network flow problem. First, create a bipartite graph \(G = (X \cup C, E)\), where \(X\) is the set of variables, \(C\) is the set of clauses, and \(E = \{(x_i, c_j): x_i \in c_j\}\). Then \(\phi\) is satisfiable if there exists a perfect matching in this graph. Let’s see how.
Proof. Suppose there exists a perfect matching in \(G\), then for every clause there is a variable which we match the clause with. Set this variable to True. (If it is the negation of the variable that appears in the clause, set the negation of the variable to True). This is the assignment that satisfies \(\phi\).
Now we will prove that such perfect matching always exists. By Hall’s Marriage Theorem, \(G\) has a perfect matching if and only if \(\|N(S)\| \geq \|S\|\) for all \(S \subseteq C\), where \(N(S)\) denotes the neighbour of \(S\) (one edge away from any vertex in \(S\)). Let \(S\) be any subset of \(C\) such that \(\|S\| = k\) for some \(k \in \mathbb{N}\). Since each clause has exactly 4 literals, there are 4 edges that connect to each clause, hence \(4k\) edges entering \(S\), and there are \(4k\) edges leaving \(N(S)\). Since every variable appears at most 4 times, each variable in \(N(S)\) has at most 4 edges leaving it. Hence \(\|N(S)\| \geq k \Rightarrow \|N(S)\| \geq \|S\|\). Thus, there always exists a perfect matching for any \(\phi\) in \({\sf 4CNF_4}\).
Solving the perfect matching problem using network flow takes polynomial time using Ford-Fulkerson or faster algorithms. Thus \({\sf 4CNF_4}\) is in \({\cal P}\). Since \({\cal P} \subseteq {\cal NP}\), the problem is also in \({\cal NP}\).
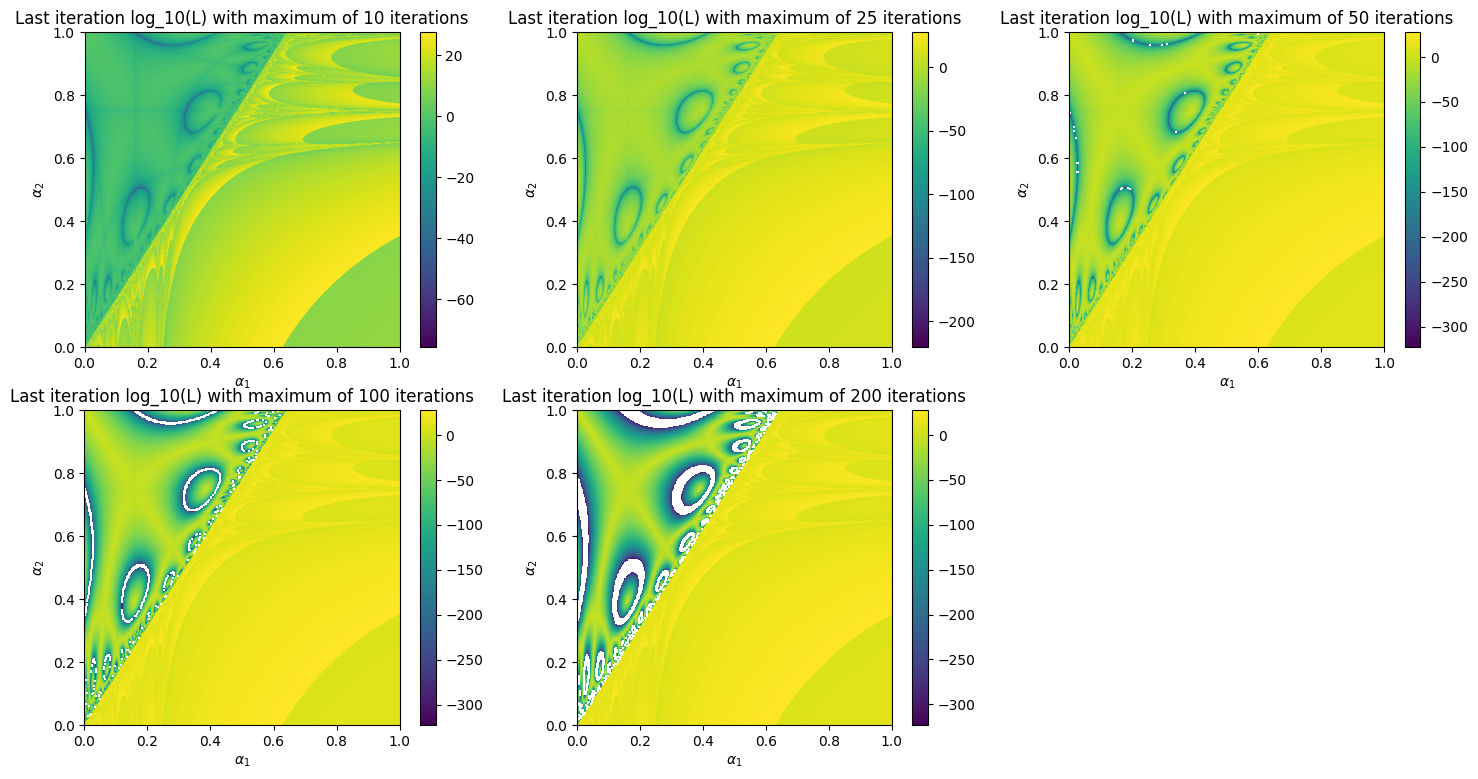
Boundary of neural network trainability is fractal
There was this assignment question which I believe was based on this paper. As the use of neural networks explode in the past few years, we were all trying make more and more powerful applications of it, and it’s not until recently that people begin to look back on what’s really going on in these networks. This result – boundary of neural network is fractal – is particularly interesting. Consider this simple neural network that is defined as
\[f(x; w_1, w_2) = w_2w_1x\]with \(x, w_1, w_2 \in \mathbb{R}\). Use the squared error loss \(l(y, t) = \frac{1}{2}\|y - t\|^2\), use the range of learning rates \(\alpha_1, \alpha_2 \in [0, 1]\) with a step size of 0.001, and use the initial weights \((w_1(0), w_2(0)) = (2.5, 2)\), plot the landscape of \(\log_{10}L\) where \(L\) is the population loss. Fractals at the boundary! [Google Colab Source Code]